卷积神经网络技巧总结
从变形卷积核、可分离卷积?卷积神经网络中十大拍案叫绝的操作。中梳理提取补充.
前提名词
feature map: 特征图, 卷积核的输入和输出都被称为feature map
卷积核技巧
0x01 多个小卷积核代替大卷积核
之前的观念是越大的卷积核感受野(receptive field)越大, 看到的信息越多, 提取的特征越好, 但存在问题:
参数剧增, 计算性能降低
不利于模型深度的增加
使用多个小卷积核代替单个大卷积核, 如在vgg和Inception网络中, 使用两个 3×3 卷积核组合代替一个 5×5 卷积核(原来的一层变为两层). 好处:
参数减少: 5×5×1 减少为 3×3×2 , 参数减少, 效率提高.
这种做法有效的原因:
在VGG网络的论文中, 除开网络本身, 最大的贡献来自于对卷积叠加的观察:
5×5卷积核的正则等效于两个3×3卷积核, 7×7卷积核的正则等效于三个3×3卷积核, 如下图所示
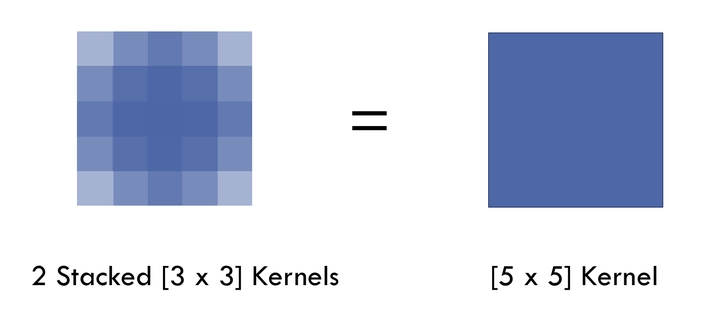
因此, 使用这种小卷积核叠加代替大卷积核有两个好处:
大幅减少参数数量
本身带有正则性质, 更能学习一个具有鲁棒性的模型
0x02 多尺寸卷积核代替单尺寸卷积核
传统的CNN网络都是层叠式网络, 每层都只使用一个卷积核. VGG网络使用了大量的3×3卷积核. 在Inception网络中, 对于同一层的feature map, 使用多个不同尺寸的卷积核, 提取出不同的特征, 再将这些特征合并起来(在通道维度上). 不同角度的特征的表现一般比单一卷积核要好.

存在的问题:
参数量比单核多很多, 模型训练效率低下
0x03 Bottleneck, 1×1 卷积核
作用: 控制通道数量, 大幅减少神经网络的参数数量, 加快网络的训练.
在Inception网络中, 由于引入了多种尺寸的卷积核, 参数数量的爆炸, 需要使用 1×1 卷积核来减少参数的数量.

以其中一个 3×3 卷积核为例, 说明如何减少:

在卷积核之前加入一个1×1卷积核, 将通道数量由原来的256压缩到64. 经过3×3卷积核计算后, 再使用另一个1×1卷积核将通道数量恢复.
原来的 3×3 卷积核参数的数量为: 256×3×3×256=589824
使用 1×1 卷积核处理后的参数数量为: 256×1×1×64+64×3×3×64+64×1×1×256=69632
参数量降到原来的将近九分之一.
0x04 空洞卷积(Dilated convolution)
标准的 3×3 卷积核只能看到 3×3 矩形区域的大小, 为了增大卷积核的感受野, 可以在标准的卷积核里注入空洞, 使卷积核拥有更大的范围, 但卷积点仍然为9个.
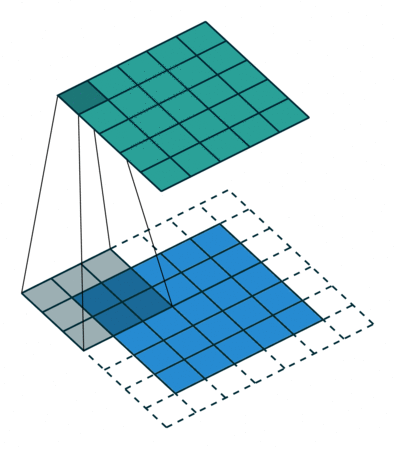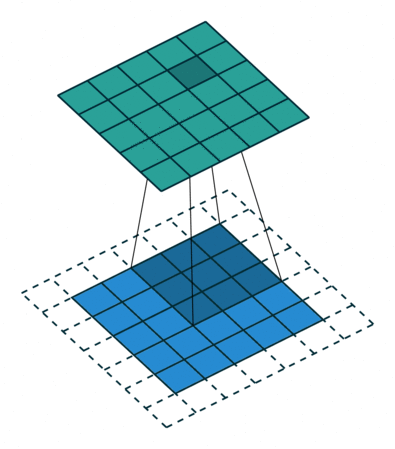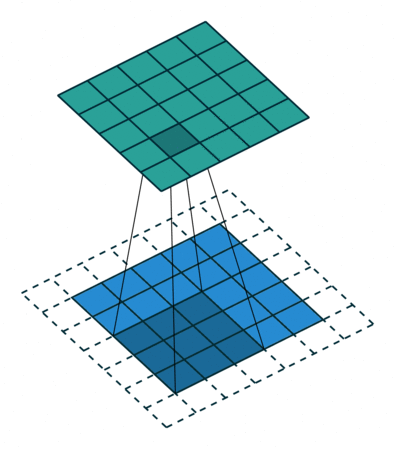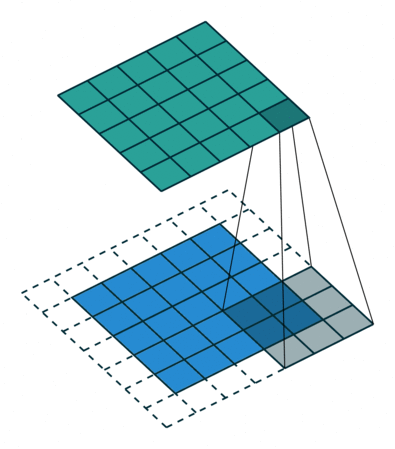
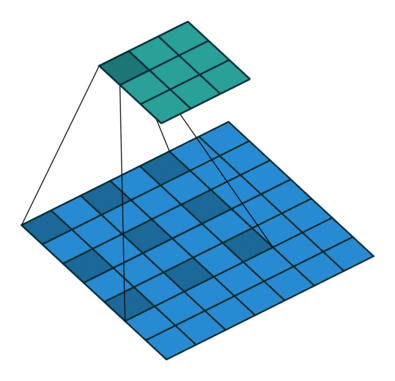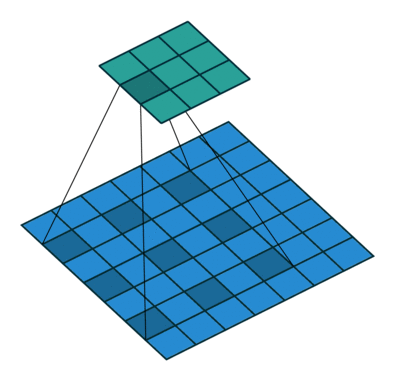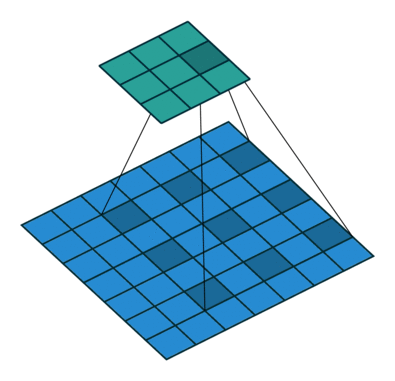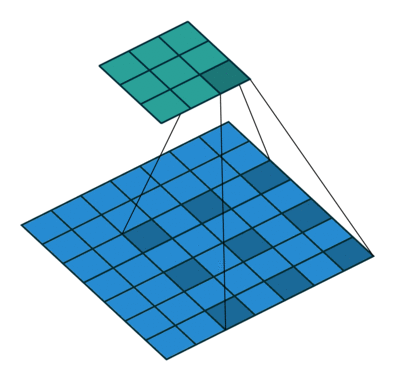
上面就是标准卷积核与空洞卷积核的工作方法. 对于空洞卷积核引入了新的超参数: dilation rate. 指的是核中点的间隔数量, 标准卷积核的dilation rate为1.
对于空洞卷积, 这篇文章如何理解空洞卷积中的回答很全面, 下面的内容也是大部分来自于这篇文章, 加以组织.
相关论文:
MULTI-SCALE CONTEXT AGGREGATION BY DILATED CONVOLUTIONS
Understanding Convolution for Semantic Segmentation
Rethinking Atrous Convolution for Semantic Image Segmentation
首先讨论空洞卷积核的问题:
The Gridding Effect
使用dilation rate为2的3×3卷积核多次叠加, 这里的叠加指的是多层相同的空洞卷积叠加作用, 则会出现下图的情况:
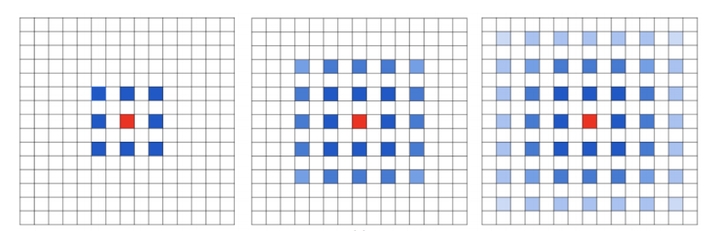
上图是多层3×3空洞卷积核的叠加, 红色为中心, 最左侧红色中心由中心和周围的蓝色点卷积得到, 而蓝色的每个点, 又由他们本身与周围的8个点卷积得到, 也就是发散到了中间的图. 如此继续叠加, 最终红色中心的值由周围若干个点卷积得到, 如右图. 蓝色越深表示卷积权重越大.
可以观察得到的是, 空洞卷积叠加之后, 等效的卷积核并不连续, 计算每个点的时候, 并不是周围所有的pixel点都用来计算了, 因此会损失信息的连续性. 这对于某些问题来说是致命的.
如何同时处理不同大小的物体关系
空洞卷积核设计的本身是为了获取大范围的信息, 但是如果采用大的dilation rate获取的信息只对大的物体具有分割效果, 对于小的物体可能就采集不到了. 因此, 如何均衡两者, 是空洞卷积设计的关键为题.
然后就是空洞卷积核的设计方法, Hybrid Dilated Convolution:
叠加卷积的dilation rate不能有大于1的公约数, 如[2, 4, 6]不是可行的三层卷积, 会出现gridding effect.
将dilation rate设计成锯齿结构, 如 [1, 2, 5, 1, 2, 5] 循环结构.
满足式子 Mi=max[Mi+1−2ri,Mi+1−2(Mi+1−ri),ri]
其中ri是i层的dilation rate, Mi是到i层最大的dilation rate, 对于最后一层n, 就有Mn=rn, [1, 2, 5]就是一个可行的方案.
锯齿状本身的性质就比较好的来同时满足小物体大物体的分割要求, 小的dilation rate关心近距离信息, 大的dilation rate关心远距离信息.
一个良好设计的空洞卷积网络能够有效的避免gridding effect:

0x05 可变形卷积核(Deformable convolution)
传统的卷积核都是正方形, 因此只能提取固定范围, 固定形状的特征. 可变性卷积核则认为卷积核的形状是可以变化的, 即卷积核应当聚集于它真正感兴趣的图像区域.

实现这种操作, 需要添加一个新的卷积核, 将这个卷积核作用于输入的feature map, 目的是学习卷积采样的位置偏移量(offset). 这个偏移参数如同正常的卷积核参数一样, 直接通过训练一起得到, 不需要额外的监督标签.
假设作用在2D的feature map上, 需要设定的这个偏移量卷积核的通道数应当是feature map通道数的两倍, 因为每个通道中的每个pixel都需要计算x方向和y方向两个方向上的偏移量.

总结下, deformable convolution由两步组成:
使用偏移量卷积核在输入的feature map上采样
将采样值与标准卷积核卷积求和, 输出新的feature map
由于单纯的使用偏移量采样, 将会产生对不连续位置求导的问题, 使用双差值方法, 将任何一个位置的输出转换为对于输入的feature map插值计算的结果.
关于可变形卷积核的详解, 包含差值方法参见Deformable Convolution Networks[译], 使用keras实现的可变卷积核Layer见kingofoz / deform-conv.
通道技巧
0x01 DepthWise
标准卷积核对输入的feature map的所有通道都会进行计算. 而DepthWise方法则将图像区域和通道分开考虑:

首先, 对输入的feature map中的每个通道, 各自进行卷积操作, 有多少个通道就有多少个filter
对经过filters处理得到的新的feature map, 使用标准的1×1卷积核跨通道操作, 得到最后的输出结果. 输出通道有多少, 就有多少个1×1卷积核.
这种操作被称为DepthWise convolution, 最大的好处就是降低了参数的数量. 因为使用了1×1卷积核, 所以一般参数量会降为直接使用标准卷积核的九分之一. 而且这种方法在降低参数的同时, 不会拉低模型的表现, 甚至会取得更好的表现.
0x02 ShuffleNet
ShuffleNet其实是两种技术的结合:
DepthWise: 上面的方法, ShuffleNet没有使用传统的卷积方法.
Group Convolution: channel分组进行卷积. 即卷积核不是对输入的feature map中的所有通道进行计算, 而是只选取一部分. 然后把所有分组的结果合并在一起作为卷积最后输出的结果. 在AlexNet中, 最先被提出.
ShuffleNet在每次对feature map进行分组卷积(Group conv)操作前, 对所有通道进行洗牌随机分组, 然后每组使用DepthWise的方式进行卷积.

上图中的(b)就是标准的Group Convolution方法, channels被平均分配到不同组里面, 然后通过全连接层来融合所有组的特征. (c)就是shuffle group conv的方法.
0x03 SEnet(通道加权计算)
标准卷积方法中, 每个卷积核都是对所有的通道进行卷积, 然后直接加和在一起, 即相当于所有通道的权重是平等的. SEnet认为不同的通道, 对模型的贡献是不同的, 因此有必要引入通道的权重参数.

网络的整体结构如上图:
对于输入的feature map即X, 其特征通道数为c1. 通过正常的卷积变换, 得到的输出的feature map的通道数量为c2. 这一步与标准卷积没有区别.
然后就要对当前的输出结果进行调整. 通过三个操作来实现:
首先是Squeeze操作, 对输出的feature map进行压缩, 通过Global Average Pooling, 将每个通道压缩成一个实数, 这样就得到了长度为c2的通道向量. 这个向量某种程度上具有全局的感受野, 表征着在特征通道上响应的全局分布.
然后是Excitation操作, 通过参数来为每个特征通道生成权重, 这里的参数是可被学习的, 被学习用来显式地建模特征通道间的相关性. 论文中把这一列特征通道向量输入两个全连接层和sigmoid转换得到.
最后是Reweight操作, 将上一步的输出的权重, 看作是进过特征选择后的每个特征通道的重要性, 然后通过乘法逐通道加权到先前的特征上, 完成在通道维度上的对原始特征的重标定.
连接技巧
0x01 ResNet(skip connection)
神经网络的层数加深时, 网络表现难以提高, 甚至会降低, 原因即熟悉的梯度消散, 使得反向传播很难训练到考前的层中. 残差网络(ResNet)通过skip connection技巧, 可以解决这个问题, 使得梯度更容易地流动到浅层的网络当中去.

至于能够起作用的原因, 可以参见这篇文章: 对ResNet的理解. 简单概括如下:
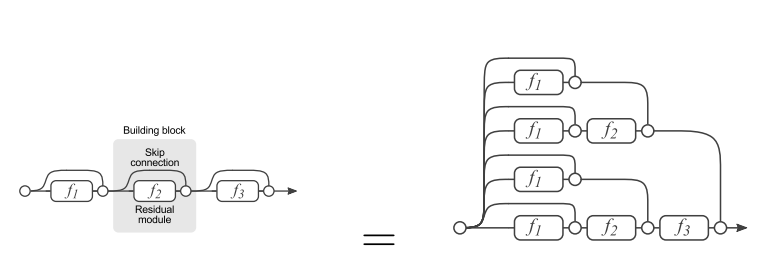
这种skip connection的方式, 可以被分解. 如图中右侧的三层串联的Residual module, 可以被分解成左侧的多种路径组合的网络. 因此, 残差网络其实是很多并行子网络的组合, 整个残差网络其实相当于一个多人投票系统Ensembling.
0x02 DenseNet
skip connection只连接了上一层的输出作为本层输出的一部分, DenseNet中的每一层输出结果都是前面所有层输出结果的叠加.
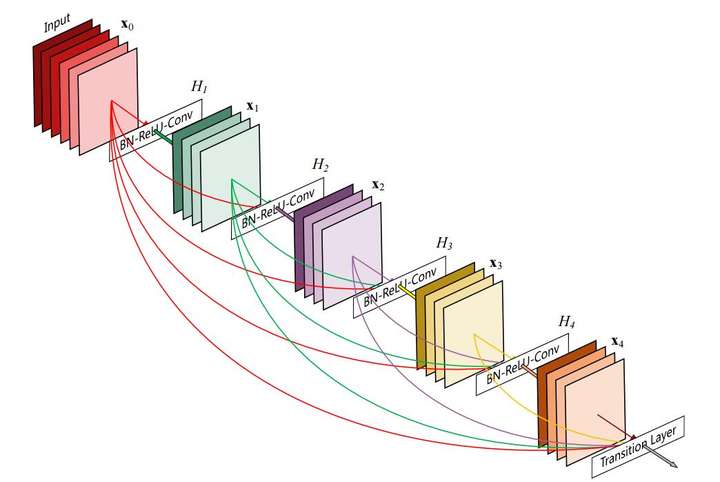
关于DenseNet的细节请阅读论文Densely Connected Convolutional Networks.
最后更新于